Diferença entre derivação implícita e parcial
Alguem sabe a diferença entre derivação implícita e parcial ?
Respostas
Euziana coelho correa
há 12 anos
Em matemática, uma derivada parcial de uma função de várias variáveis é a sua derivada com respeito a uma daquelas variáveis, com as outras variáveis mantidas constantes. Este conceito é útil no cálculo vectorial e geometria diferencial.
Suponha-se que ƒ é uma função de mais de uma variável. Para obter-se uma instância,
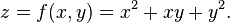
O gráfico desta função define uma superfície no espaço euclidiano. Para cada ponto sobre esta superfície, há um número infinito de linhas tangenciais. Diferenciação parcial é o ato de escolher uma dessas linhas e encontrar o seu declive. Normalmente, as linhas de maior interesse são aquelas que são paralelas ao planoxz, e aquelas que são paralelos ao plano yz(que resultam da exploração ou y ou xconstante, respectivamente.)
Para determinar o declive da linha tangente à função de P (1, 1, 3) que é paralela ao plano xz, o y variável é tratado como constante. O gráfico e este plano são mostrados à direita. No gráfico abaixo, vemos a forma como a função se comportay = 1.Ao encontrar a derivada da equação assumindo que y é uma constante, e o declive ƒ no ponto(x, y, z) é:
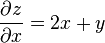
Então, em (1, 1, 3), por substituição, o declive é de 3. portanto
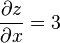
no ponto. (1, 1, 3). Ou seja, a derivada parcial de z com relação a x em (1, 1, 3) é 3.
Derivada implícita com exemplos numéricos
Antes de introduzir uma regra geral que permite obter os extremos de uma função definida por F(x,y)=0 de uma forma implícita, apresentaremos dois exemplos numéricos com funções conhecidas.
Exemplo: Consideremos a curva conhecida como Folium de Descartes, definida de forma implícita por:
F(x,y) = x³ + y³ - 3axy = 0 (a>0)
Problema: Obter o ponto da curva que está a maior distância do eixo horizontal (altura máxima).
Para resolver este problema, devemos obter o ponto de máximo de y=y(x) e a dificuldade é obter de forma explícita y=y(x). Embora exista a fórmula de Tartaglia-Cardano para resolver o problema, a expressão desta função y=y(x) é muito complicada. Existem outras situações que nem mesmo é possível explicitar y=y(x). Para contornar estes problemas, usaremos a derivação da função definida implicitamente pela curva: x³ + y³ - 3axy = 0
Crie sua conta grátis para liberar essa resposta. 🤩
Já tem uma conta?
Ao continuar, você aceita os Termos de Uso e Política de Privacidade
Francisco Mário Fagundes
há 12 anos
Na derivada implícita vc vai derivar de um lado e de outro da igualdade mas as duas icognitas serão derivadas, assim sempre que você derivar "y", vc terá que colocar uma multiplicação por y' ao lado. Já na parcial vc vai derivar primeiro em função de x, tratando as outras icognitas como constante, depois em função de y, depois de z e etc... Sempre tratando o resto das icognitas como constante... Não sou muito bom com as palavras, mas ta aí :S
Euziana coelho correa
há 12 anos
Em geral, não é necessário resolver uma equação de y em termos de x, a fim de diferenciar as funções definidas pela equação. Para ilustrar isto, consideremos a equação
xy = 1
Uma maneira de achar dy/dx é reescrever esta equação como
da qual tem-se que
Contudo, há uma outra maneira de obter esta derivada. Podemos diferenciar ambos os lados de xy = 1 antes de resolver para y em termos de x, tratando y como (não-especificado temporariamente) uma função diferenciável de x. Com esta abordagem, obtemos
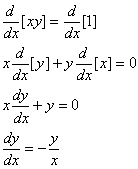
Se agora substituirmos na última expressão, obtemos
que está de acordo com . Este método para obter derivadas é chamado de diferenciação implícita.
Exemplo 1
Use a diferenciação implícita para achar dy/dx se 
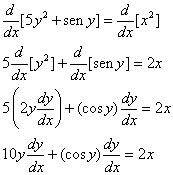
Resolvendo para dy/dx obtemos
Note que esta fórmula envolve ambos x e y. A fim de obter uma fórmula para dy/dx que envolva apenas x, teríamos que resolver a equação original para y em termos de x e, então, substituir em . Entretanto, isto é impossível de ser feito; assim, somos forçados a deixar a fórmulady/dx em termos de x e y.
Exemplo 2
Use a diferenciação implícita para achar 
se 
.
Solução. Diferenciado ambos os lados de implicitamente, obtém-se
de que obtemos
Diferenciando ambos os lados de implicitamente, obtém-se
Substituindo dentro de e simplificando, usando a equação original, obtemos
Ainda com dúvidas?
Envie uma pergunta e tenha sua dúvida de estudo respondida!
